Hilfe bei einer Matrizen Aufgabe (Klausur Korrektur)

[DarkRiverCoke]

Hallo,
ich habe folgende Aufgabe gehabt & die komplett erfolgreich daneben gehauen.
Wie ich die jetzt verbessern soll,weiß ich nicht wirklich,sonst hätte ich die ja wohl richtig gerechnet.
Da hier ein paar nette Leute anwesend sind,die mir schon öfters geholfen haben,dachte ich mir warum nicht.Gibt ja noch ein paar Hilfsbereite.
Falls jemand ansatzweise eine Lösung zu den Aufgaben hinbekommt (auch wenn's nur nen reiner Versuch ist) würde ich mich extrem freuen.
Vielen lieben Dank.

[Nuebel]

Für Aufgabe a.1 musst du einfach nur 20 mit der Matrix (rechte Tabelle) multiplizieren:



und dann die Komponenten der Zeilenvektoren addieren. Also:
Für G1: 380 + 280 + 400 = 1060 ME
Für G2: 460 + 260 + 500 = 1220 ME
Für G3: 420 + 360 + 420 = 1200 ME


Aufgabe a.2 wird schon etwas umfangreicher; hier hast du Einiges mehr zu schreiben ^^. Ich werde es nur für das erste Parfüm zeigen. Für die beiden anderen ist der Weg derselbe, nur mit anderen Zahlen.
Da hier nach den Basismischungen gefragt wird, müssen wir uns mit der linken Tabelle beschäftigen. Die Frage lautet, wie viele Mengeneinheiten von den jeweiligen Basismischungen benötigt man, um eine Mengeneinheit von Parfüm 1 herzustellen? Dazu stellen wir die simple Gleichung auf:



In der Aufgabenstellung wird uns verraten, wie sich B1, B2 und B3 zusammensetzen (linke Tabelle), also ersetzen wir es in der oben gezeigten Gleichung:



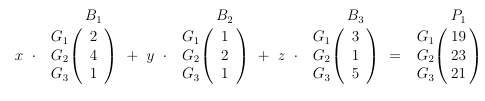
Das sieht doch schon einmal besser aus, denn jetzt lässt sich sehr einfach ein Lineares Gleichungssystem bilden:



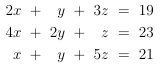
Wenn wir jetzt die 1. Gleichung mit -2 multiplizieren und dann mit der 2. Gleichung addieren, hauen wir sofort zwei Unbekannte raus, x und y. Es bleibt:



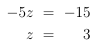
Schön, jetzt wo z bekannt ist können wir es in unser Ausgangsgleichungssystem einsetzen und erhalten:



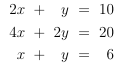
Jetzt knöpfen wir uns die nächste Unbekannte vor. Ich habe mich für y in der ersten Gleichung entschieden. Nach dem Umformen sieht es so aus:



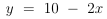
Dieses y setzen wir jetzt in irgendeine andere Gleichung ein, zum Beispiel in der dritten, und formen nach x um:



Dieses x können wir wiederum in die y-Gleichung einsetzen und erkennen, dass y gleich 2 ist.

Jetzt kennen wir alle drei Unbekannte und diese jetzt zur Probe in die klobige Gleichung oben mit den drei Spaltenvektoren einsetzen und schauen, ob es stimmt:



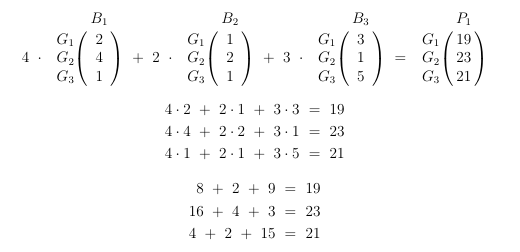
Stimmt alles. Für 1 Mengeneinheit von Parfüm 1 brauchen wir also 4 Mengenheiten von Basismischung 1, 2 Mengeneinheiten von Basismischung 2 und 3 Mengeneinheiten von Basismischung 3.
Die Lösung lasst sich ebenfalls als Matrix bzw. Spaltenvektor darstellen. Lägen jetzt bereits die Ergebnisse für Parfüm 2 und 3 vor, wäre das Ergebnis eine 3x3-Matrix. Diese multipliziert mit der linken Matrix auf dem Aufgabenblatt ergäbe dann die rechte Matrix auf dem Aufgabenblatt.



Hier wäre die Probe dann die geliebte nicht kommutative Matrizenmultiplikation:




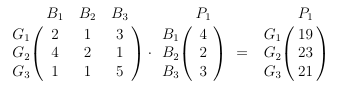
Die restlichen Aufgaben werde ich mir bei Gelegenheit (wahrscheinlich morgen) anschauen. Du kannst bis dahin ja schon einmal etwas Eigeninitiative zeigen und dein Ansatz posten.



Edit: Ein LaTeX-Plugin wäre schon was, das Aufnehmen und Hochladen von Screenshots nervt ab einer gewissen Anzahl.

Edit 2: Habe noch etwas Zeit gefunden und weiter gemacht.



Die komplette Lösungsmatrix für Aufgabe a lautet:



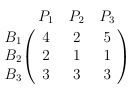
Ob ich richtig gerechnet habe, kannst du überprüfen mit:





Aufgabe b:
Wir müssen herausfinden, wie viele Basismischungen für die Aufträge der beiden Kunden draufgehen. Also stellen wir uns hier wieder etwas Schönes auf:



Das könnte man jetzt wie oben ausrechnen. Oder man bedient sich wieder der Matrizenmultiplikation:



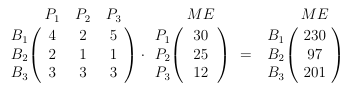
(Hier sieht man auch, dass es sinnvoll ist, Matrizen zu beschriften. Das hilft ungemein beim Interpretieren.)

Das war's zum ersten Kunden. Der zweite Kunde bestellt nur das Parfüm 3; 150 ME davon.
Hier müssen wir jetzt wirklich den Weg über die Spaltenvektoren gehen. Das heißt:



Das ist der Bedarf für Kunde 2. Jetzt wollen wir aber wissen, wie viele Mengeneinheiten der Basismischungen für beide Aufträge vorrätig sein müssen. Das ist simple Addition:



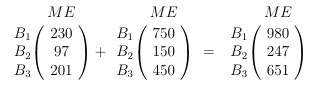
Für beide Aufträge brauchen wir von Basismischung 1 insgesamt 980 Mengeneinheiten. Es sind aber nur 900 Mengeneinheiten vorrätig. Damit haben wir schon gezeigt, dass der Hersteller nicht sofort beide Kunden beliefern kann. Weiter geht's mit der Berechnung der fehlenden Grundsubstanzen. Subtraktion:



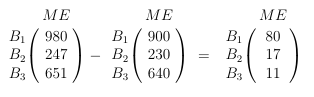
Jetzt brauchen wir wieder die linke Matrix aus der Aufgabenstellung. Diese gibt ja an, wie viele Grundsubstanzen für die jeweiligen Basismischungen notwendig sind. Wieder einmal kommt die Matrizenmultiplikation zum Einsatz:



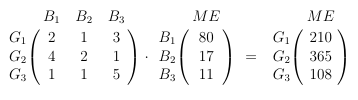
Fertig! Es müssen 210 ME von G1, 365 ME von G2 und 108 ME von G3 nachbestellt werden.


Aufgabe c.
Hier muss zunächst die Transponierte der linken Matrix aus der Aufgabenstellung bestimmt werden: (die Matrix gibt nach wie vor dieselben Informationen preis, nur in einer anderen Darstellung)



Jetzt wird es wieder einfach und es wird auf Bekanntes zurückgegriffen. Die Werte aus der Aufgabe als Spaltenvektor mit der eben bestimmten Transponierten multiplizieren:



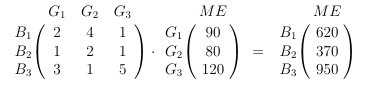
Mit den vorhandenen Grundsubstanzen lassen sich entweder 620 ME von B1 oder 370 ME von B2 oder 950 ME von B3 herstellen.

Edit 3: Bei Aufgabe c habe ich mich geirrt. War gestern wohl doch schon zu spät. Hier muss die Determinante berechnet werden. Wenn diese ungleich 0 ist, wird die Inverse der Matrix bestimmt und mit der anderen multipliziert. Werde es noch einmal editieren, wenn ich am Pc bin.

[DarkRiverCoke]

@Nuebel

Danke für deine ausführliche Hilfe & dass Du dir die ganze Mühe gemacht hast.
Finde ich super von Dir! Großen Dank

[freulein]

Sollte jemals der Titel: "Help Champion OF U-LABS" vergeben werden, dann möchte ich vorschlagen, daß Nuebel den bekommt, wenigstens beim ersten Mal. Selbst wenn ihm das Durchrechnen der Aufgabe Spaß machte, was offensichtlich der Fall war, ist doch das zusätzlich noch Nötige, das ganze Schreiben, Screenshotten und Reinstellen, eine ziemliche Arbeit.