Fibonacci-Zahlen in C berechnen

Eine Funktion zur Berechnung der Fibonacci-Zahlen schreiben – Diese recht beliebte Aufgabe wird gerne von Uni-Professoren und Berufsschullehrern von Fachinformatikern gestellt. Die Gründe liegen auf der Hand: Anhand einer überschaubaren Logik lässt sich die Funktionsweise von Rekursion demonstrieren. Und außerdem Ihre Nachteile, da die rekursive Berechnung größerer Fibonacci-Zahlen rechenintensiv ist. Folgender Artikel zeigt die Umsetzung einer einfachen Konsolenanwendung in der Programmiersprache C zur Berechnung dieser Zahlen.

Was ist eine Fibonacci-Zahl?

Kurz gesagt dient sie zur Berechnung von Wachstumsvorgängen. Etwas detaillierter lässt sie sich an folgendem Beispiel erklären: Angenommen, die Kaninchen in einem Stall erhalten jeden Monat zwei gegengeschlechtliche Zwillinge als Nachwuchs. Unter der Annahme, dass die Kaninchen niemals sterben oder aufhören sich weiter fortzupflanzen, entspricht die Anzahl der Kaninchenpaare im Stall nach n Monaten die n-te Fibonacci-Zahl – in unserem Beispiel mit der Funktion F(n).

Haben wir zu Beginn nur ein einzelnes Paar Kaninchen, verändert sich der Bestand in den ersten beiden Monaten nicht: F(1) = 1 und F(2) ist ebenfalls 1 – denn dieses Paar wird erst nach dem Alter von zwei Monaten zeugungsfähig sein. Im dritten Monat (n = 3) wird ein weiteres Kaninchen gezeugt, sodass nun insgesamt 2 Paare (Jeweils 1 Paar Eltern und Kinder) vorhanden sind – F(3) ergibt daher 2. Nachdem vierten Monat leben F(4) = 3 Paare, das zweite Zwillingspaar der Eltern.

Nun wird es interessant: Im 5. Monat bekommt nicht nur das ursprünglich erste Paar Nachwuchs, sondern auch deren erste Kinder – Somit leben nun 5 Kaninchen. Monat 6 bring insgesamt drei neue Paare, da hier zu den eben genannten noch das zweite Nachwuchspaar dazu kommt. So setzt sich das Wachstum weiter fort.

C-Funktion zur Berechnung der n-ten Fibonacci-Zahl

Die Anzahl der lebenden Paare im Monat n + 1 entspricht allgemein gesagt der Anzahl der Paare, die im vorherigen Monat (n) gelebt haben. Dazu werden die neu geborenen Addiert. Durch die Fortpflanzung alle zwei Monate ist die Anzahl der Kinder gleich wie die Anzahl der Paare, welche vor zwei Monaten lebten. Daraus lässt sich die Formel

f(n) = f(n - 1) + f(n - 2)

ableiten. Wobei diese nur gilt, wenn n größer oder gleich 2 ist – Denn in den ersten beiden Lebensmonaten wird kein Nachwuchs gezeugt. f(1) ist somit 1 und f(2) = 2. Negative Fibonacci-Zahlen kann es nicht geben. Der Prototyp einer Funktion zur Implementierung dieser Formel könnte daher wie folgt aussehen:

int calculate_fibonacci_number(int number);

Die ganze Zahl number entspricht unserem Eingangswert n. Als Rückgabewert wird die ebenfalls ganzzahlige Fibonacci-Zahl geliefert. In der Funktion müssen wir zunächst mit If-Abfragen die oben genannten Ausnahmefälle abfangen:

// Von 0 bis 2 entspricht die Fibonacci-Zahl der Eingabe
if (number >= 0 && number < 2) {
	return number;
}

Nun gelangen wir zur eigentlichen Berechnung der Fibonacci-Zahl. Die Implementierung gleicht dabei obiger Formel:

return calculate_fibonacci_number(number - 1) + calculate_fibonacci_number(number - 2);

Die gesamte Funktion sieht daher so aus:

int calculate_fibonacci_number(int number) {
	// Von 0 bis 2 entspricht die Fibonacci-Zahl der Eingabe
	if (number >= 0 && number < 2) {
		return number;
	}
	return calculate_fibonacci_number(number - 1) + calculate_fibonacci_number(number - 2);
}

Mit einem einfachen Beispielprogramm lässt sich die Funktion auf vom Benutzer eingegebene Zahlen anwenden:

// Beinhaltet Funktionen zur Ein- und Ausgabe wie printf und scanf - Der Name steht für StandardInputOutput
#include <stdio.h>
// In C müssen die Prototypen getrennt von der Implementierung definiert werden. Bei größeren Anwendungen verschiebt man diesen Teil in eine Header-Datei (*.h)
int calculate_fibonacci_number(int number);

int main(void) {
	printf("Fibonacci-Zahl berechnen\n\nBitte eine Zahl groesser 0 eingeben: ");
	int input_number = 0;
	scanf_s("%d", &input_number);

	// Eingegebene Zahl validieren und falls diese ungültig ist den Nutzer zur erneuten Eingabe auffordern
	if (input_number < 0) { system("cls"); printf("Fehler: Die Fibonacci-Zahl kann nur von ganzen Zahlen berechnet werden, die größer als 0 sind! Bitte Eingabe wiederholen."); main(); } // Ist die Eingabe gültig, berechnen wir die dazugehörige Fibonacci-Zahl und geben sie aus int fibonacci_number = calculate_fibonacci_number(input_number); printf("Die Fibonacci-Zahl von %d lautet: %d\n\nBeliebige Taste zum beenden druecken...", input_number, fibonacci_number); getch(); } // Die eigentliche Implementierung der Funktion, die unsere Fibonacci-Zahl berechnet int calculate_fibonacci_number(int number) { // Von 0 bis 2 entspricht die Fibonacci-Zahl der Eingabe if (number >= 0 && number < 2) {
		return number;
	}
	return calculate_fibonacci_number(number - 1) + calculate_fibonacci_number(number - 2);
}

[box type=“info“ align=“aligncenter“ ]Zu beachten ist, dass diese Implementierung Windows-Spezifische Aufrufe wie cls verwendet. Sie sollten in dieser Form nur zu Lernzwecken verwendet werden – denn ein Angreifer könnte die Umgebungsvariablen manipulieren und dadurch ggf. Schadcode mit erhöhten Rechten ausführen. Siehe dazu Sicherheitslücken von Umgebungsvariablen[/box]

Rekursive vs. iterative Lösung im Vergleich

Im obigen Beispiel wird die Fibonacci-Zahl rekursiv berechnet. Die Funktion calculate_fibonacci_number ruft sich also selbst auf, um beispielsweise die vorherige Zahl zu berechnen. Diese Lösung ist wie man sieht sehr einfach und besteht nur aus einer Zeile Code. Rekursive Funktionen bringen allerdings zwei Probleme: Als Entwickler muss man penibel auf die Abbruchbedingung achten, um nicht in einer Endlosschleife zu landen. Vor allem bei komplexeren Funktionen wird dies schnell übersehen bzw. nicht vollständig eingebaut. Darüber hinaus erzeugen rekursive Aufrufe zusätzlichen Overhead, sodass diese Lösungen nicht selten eine schlechtere Performance aufweisen als iterative Ansätze.

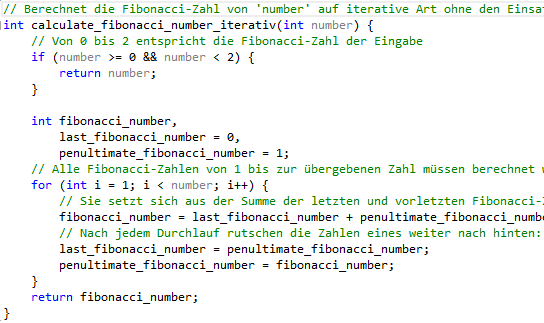
// Die eigentliche Implementierung der Funktion, die unsere Fibonacci-Zahl berechnet
int calculate_fibonacci_number_iterativ(int number) {
	// Von 0 bis 2 entspricht die Fibonacci-Zahl der Eingabe
	if (number >= 0 && number < 2) {
		return number;
	}

	int fibonacci_number, 
		last_fibonacci_number = 0, 
		penultimate_fibonacci_number = 1;
	// Alle Fibonacci-Zahlen von 1 bis zur übergebenen Zahl müssen berechnet werden
	for (int i = 1; i < number; i++) {
		// Sie setzt sich aus der Summe der letzten und vorletzten Fibonacci-Zahl zusammen
		fibonacci_number = last_fibonacci_number + penultimate_fibonacci_number;
		// Nach jedem Durchlauf rutschen die Zahlen eines weiter nach hinten: Die aktuelle wird zur letzten und die letzte zur Vorletzten
		last_fibonacci_number = penultimate_fibonacci_number;
		penultimate_fibonacci_number = fibonacci_number;
	}
	return fibonacci_number;
}

Bei kleineren Zahlen ist der Unterschied derart gering, dass er bedenkenlos vernachlässigt werden kann. Werden jedoch größere Zahlen berechnet, macht sich der Overhead bemerkbar: Die Fibonacci-Zahl zu 35 wird rekursiv in 840 ms berechnet. Bei 40 als Input sind es schon rund 9,4 Sekunden. Berechnen wir die Fibonacci-Zahl von 42, benötigt die rekursive Variante mehr als satte 24 Sekunden. Die iterative Lösung dagegen ist derart schnell, dass ihre Ausführungszeit in Millisekunden nicht messbar ist – Sie liegt wohl im Nanobereich.

[box type=“info“ align=“aligncenter“ ]Fibonacci-Zahlen werden sehr schnell sehr groß, wie man anhand dieser Tabelle sehen kann: Schon ab einer Eingangszahl von 31 liegt die Fibonacci-Zahl im Millionenbereich, bei 45 überschreitet sie die Grenze von einer Milliarde. Ein 32 Bit Integer kann jedoch nur maximal den Wert 2.147.483.647 (signed) annehmen. Bei größeren Werten setzt er sich wie ein analoger Tacho auf 0 zurück und liefert falsche Ergebnisse – ein schwer auffindbarer Fehler! Zur Arbeit mit größeren Zahlen sollte daher größere und genauere Alternativen wie float, double oder ggf. sogar long double verwendet werden. [/box]